7 Tests, Zusammenhangsmaße und Regression

7.1 Statistisches Testen

Ziel ist mit Stichprobendaten allgemein gültige Aussagen über die Grungesamtheit treffen zu können. Dazu werden Hypothesentests durchgeführt häufig in Form von Signifikanztests.

Allgemeines Vorgehen bei Signifikanztests:

Null- und Alternativhypothese formulieren ($H_0\ und\ H_a$)
Wahl eines passenden Tests (z.B. t-Test, …)
Bestimmung des Signifikanzniveaus $\alpha$
Berechnung des Wertes der Beobachtung (z.B. t-Wert, …)
Treffen der Testentscheidung

7.1.1 $\chi^2$-Test

Gleichverteilungstest - sind Kategorien gleich häufig?
- $H_0$: Kategorien sind gleichhäufig
- $H_a$: Kategorien sind nicht gleichhäufig
Unanghängigkeitstest - sind zwei nominale Merkmale unabhängig voneinander?
- $H_0$: Merkmale sind unabhängig
- $H_a$: Merkmale sind abhängig

Die Funktion chisq.test() berechnet je nach Eingabe einen entsprechenden Test. Eingabeparameter sind dabei im Format von table():

Gleichverteilungstest:
- table(x)
Unanghängigkeitstest:
- table(x, y)

Beispiel

df_yoga <- read.table("data/YogaPilates.txt", header = TRUE)

Gleichverteilungstest:

tab <- table(df_yoga$gruppe)
chisq.test(tab)

    Chi-squared test for given probabilities

data:  tab
X-squared = 4.55, df = 2, p-value = 0.1028

Unanghängigkeitstest:

tab2 <- table(df_yoga$gruppe, df_yoga$geschl)
chisq.test(tab2)

    Pearson's Chi-squared test

data:  tab2
X-squared = 0.99223, df = 2, p-value = 0.6089

7.1.2 t-Test

Varianten des t-Tests:
- Einstichproben t-Test: Vergleich eines Mittelwerts mit einer Konstante
  - $H_0$: Mittelwert weicht nicht von Konstante ab
  - $H_a$: Mittelwert weicht von Konstante ab
- Zweistichproben t-Test: Vergleich von zwei Mittelwerten aus ab- oder unabhängigen Stichproben
  - $H_0$: Mittelwerte weichen nicht voneinander ab
  - $H_a$: Mittelwert weichen voneinander ab

Alle Varianten des t-Tests werden mit t.test() berechnet.

Zwei Möglichkeiten der Dateneingabe
- t.test(Werte1, Werte2)
- t.test(Werte ~ Faktor)
Optionale Argumente:
- alternative: Richtung der Testung ("two.sided", "greater", "less")
- mu: Konstante, gegen die getestet werden soll
- paired: unabhängige (FALSE) oder abhängige (TRUE) Stichproben?
- var.equal: Annahme von Varianzgleichheit gegeben (ja = TRUE)?
- conf.level: Konfidenzniveau

Beispiel

t-Test - Einstichprobentest

t.test(df_ex$Revise, mu = 5, alternative = "greater")

    One Sample t-test

data:  df_ex$Revise
t = 8.4094, df = 101, p-value = 1.395e-13
alternative hypothesis: true mean is greater than 5
95 percent confidence interval:
 16.41727      Inf
sample estimates:
mean of x 
 19.22549

t-Test - Zweistichprobentest - abhängige Stichproben

t.test(df_ex$Note, df_ex$Note_2, paired = TRUE)

    Paired t-test

data:  df_ex$Note and df_ex$Note_2
t = 3.3339, df = 101, p-value = 0.001198
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 0.2382293 0.9382413
sample estimates:
mean difference 
      0.5882353

t-Test - Zweistichprobentest - unhängige Stichproben

t.test(df_ex$Revise ~ df_ex$bestanden)

    Welch Two Sample t-test

data:  df_ex$Revise by df_ex$bestanden
t = 4.4799, df = 96.44, p-value = 2.053e-05
alternative hypothesis: true difference in means between group bestanden and group durchgefallen is not equal to 0
95 percent confidence interval:
  6.707692 17.380155
sample estimates:
    mean in group bestanden mean in group durchgefallen 
                   23.35821                    11.31429

7.1.3 ANOVA

Vergleich von Mittelwerten von mehr als zwei Gruppen:

Abhängige (within ANVOA) oder unabhängige (between ANOVA) Stichproben?
Post-hoc-Tests für genauere Gruppenvergleiche
Mehrfaktorielle ANOVA für mehrere unabhängige Variablen und deren Interaktion

Paket ez

Varianzanalysen lassen sich in R auf viele (auch umständliche Arten) berechnen. Das Paket ez bietet mit der Funktion ezANOVA() eine benutzerfreundliche Möglichkeit zum Durchführen von ANOVAs Wichtige Argumente:

data: Dataframe
dv: Abhängige Variable
wid: Variable, die die Fälle im Dataframe eindeutig unterscheidet (ID-Variable)
between: Zwischensubjektfaktoren, anzugeben als Liste mit .(Faktor 1, Faktor 2, …)
within: Innersubjektfaktoren, anzugeben als Liste mit .(Faktor 1, Faktor 2, …)
type: Art der Quadratsummenzerlegung (Typ 2 ist Default, Typ 3 ist der Standard von SPSS)

Beispiel

df_yoga_clean <- read.table("data/YogaPilates.txt", header = TRUE) |> na.omit()
library(ez)

Einfaktorielle ANOVA - Between-Faktor

ezANOVA(data = df_yoga_clean, dv = zufri, wid = vp, between = gruppe, type = 2)
Coefficient covariances computed by hccm()
$ANOVA
  Effect DFn DFd        F         p p<.05        ges
1 gruppe   2 113 3.610455 0.0302038     * 0.06006367

$`Levene's Test for Homogeneity of Variance`
  DFn DFd       SSn      SSd        F         p p<.05
1   2 113 0.7027865 71.73687 0.553515 0.5764761

Post-hoc-Tests

Post-hoc-Tests für paarweise Gruppenvergleiche können mit pairwise.t.test(x, g, p.adjust.method = "…", paired = …, …) ausgegeben werden.

x: Vektor der abhängigen Variable
g: Vektor der unabhängigen Variable (Gruppe)
p.adjust.method: Korrekturmethode für multiples Testen?p.adjust
paired: Innersubjekt(within)- (TRUE) oder Zwischensubjekt(between)faktoren (FALSE)?

pairwise.t.test(df_yoga_clean$zufri, df_yoga_clean$gruppe, 
                p.adjust.method = "bonferroni", paired = FALSE)

    Pairwise comparisons using t tests with pooled SD 

data:  df_yoga_clean$zufri and df_yoga_clean$gruppe 

        kontroll pilates
pilates 1.000    -      
yoga    0.062    0.043  

P value adjustment method: bonferroni

Einfaktorielle ANOVA: Within-Faktoren

z.B. „Unterscheiden sich die Zufriedenheitswerte der Teilnehmenden vor und nach dem Training?“
„Problem“: in diesem Datensatz haben wir keine within-Faktoren -> angst sei die Zufriedenheitsmessung vor der jeweiligen Intervention (Gruppe) -> Dadurch kann der Faktor Zeit mit aufgenommen werden

df_yoga <- read.table("data/YogaPilates.txt", header = T)
head(df_yoga, n=5)
    vp geschl alter  gruppe zufri angst
1 AA21      w    37    yoga     5     1
2 AW14      m    31 pilates     4     4
3 BA55      w    38    yoga     4     2
4 BA76      m    35    yoga     5     2
5 BP45      w    23 pilates     4     1

# Zufriedenheit t_1
df_yoga$zufri_t1 <- df_yoga$angst
# Zufriedenheit t_2
df_yoga$zufri_t2 <- df_yoga$zufri

head(df_yoga, n=5)
    vp geschl alter  gruppe zufri angst zufri_t1 zufri_t2
1 AA21      w    37    yoga     5     1        1        5
2 AW14      m    31 pilates     4     4        4        4
3 BA55      w    38    yoga     4     2        2        4
4 BA76      m    35    yoga     5     2        2        5
5 BP45      w    23 pilates     4     1        1        4

Einfaktorielle ANOVA: Within-Faktoren

Achtung!: Für ANOVA müssen auch within-Faktoren ins Long-Format gebracht werden

library(reshape2)
df_yogaL <- melt(df_yoga, 
                 id.vars = c("vp", "geschl", "alter", "gruppe", "angst","zufri"),
                 variable.name = "Zeitpunkt", 
                 value.name = "Zufriedenheit")
head(df_yogaL, n=5)
    vp geschl alter  gruppe angst zufri Zeitpunkt
1 AA21      w    37    yoga     1     5  zufri_t1
2 AW14      m    31 pilates     4     4  zufri_t1
3 BA55      w    38    yoga     2     4  zufri_t1
4 BA76      m    35    yoga     2     5  zufri_t1
5 BP45      w    23 pilates     1     4  zufri_t1
  Zufriedenheit
1             1
2             4
3             2
4             2
5             1

Einfaktorielle ANOVA: Within-Faktoren

Deskriptive Analysen

library(psych)
describeBy(df_yogaL$Zufriedenheit, group = df_yogaL$Zeitpunkt)

 Descriptive statistics by group 
group: zufri_t1
   vars   n mean   sd median trimmed  mad min max range
X1    1 120 2.49 1.33      2    2.36 1.48   1   5     4
   skew kurtosis   se
X1 0.49    -0.95 0.12
--------------------------------------------- 
group: zufri_t2
   vars   n mean   sd median trimmed  mad min max range
X1    1 116 3.54 1.03      4    3.59 1.48   1   5     4
    skew kurtosis  se
X1 -0.42    -0.56 0.1

Vergleiche Output der between-ANOVA für die Interpretation der Werte
Bei mehr als zwei Stufen des Innersubjektfaktors wird der Mauchly-Test (Test auf Sphärizität) mit ausgegeben

library(ez)
ezANOVA(na.omit(df_yogaL), dv = Zufriedenheit, wid = vp, 
        within = .(Zeitpunkt))

7.2 Zusammenhangsmaße

Kovarianz:

nichtstandardisiertes Zusammenhangsmaß
monotoner Zusammenhang

Korrelationskoeffizient (nach Bravais-Pearson):

standardisiertes Zusammenhangsmaß
linearer Zusammenhang
Variablen mindestes intervallskaliert

Beispieldatasatz

Wie hängen die Itemantworten zusammen?

df_exam <- read.table("data/Daten.txt", header = TRUE)
head(df_exam, c(5,8))
  Person item1 item2 item3 item4 item5 item6 item7
1      1     3     2     3     2     2     1     4
2      2     4     1     4     3     1     1     4
3      3     3     1     3     3     1     1     3
4      4     2     2     2     2     2     2     2
5      5     2     2     2     2     1     1     3

Kovarianz und Korrelation - zwei Variablen

Für die Berechnung der Korrelation wird cor() verwendet, für die Berechnung der Kovarianz cov()
Argumente bei cor(x, y, method = "…", use = "…")
- x und y: Datenvektoren
- method: Welche Korrelation soll berechnet werden?
  - Produkt-Moment-Korrelation ("pearson"), Rangkorrelation $\rho$ ("spearman") oder Rangkorrelation $\tau$ ("kendall")
- use: Umgang mit fehlenden Werten (siehe nächste Folie)
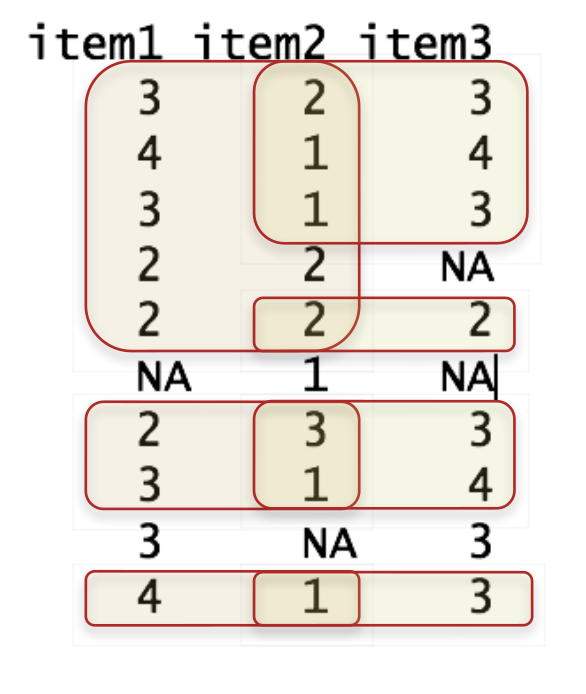
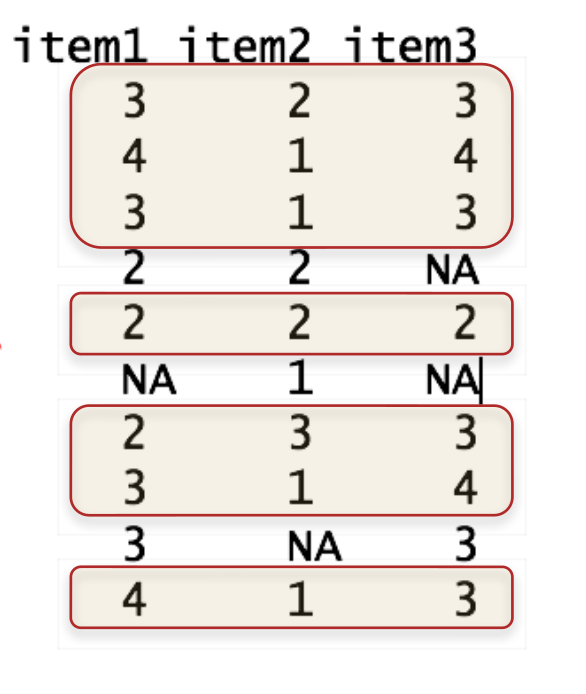
use = "…" regelt den Umgang der Korrelationsfunktionen mit fehlenden Werten
- "everything": Kein Umgang mit fehlenden Werten $\rightarrow$ bei einzelnen fehlenden Werten wird keine (einzige) Korrelation berechnet (Ergebnis: NA)
- "pairwise": Korrelationen werden jeweils mit den vollständigen Fällen pro Variablenpaar berechnet (paarweiser Ausschluss)
- "complete": Korrelationen werden nur aus in allen Variablen vollständigen Fällen berechnet (fallweiser Ausschluss)

everything	pairwise	complete

Funktion cor.test()

cor.test(x, y, method = "…", use = "…", alternative = "…", conf.level = …, …) für Inferenzstatistik bei Korrelationen
- x, y, method, use: Siehe cor()
- alternative: Ist die Testrichtung…
  - Ungerichtet (default): "two.sided"
  - einseitig: Positive Korrelationshypothese "greater"
  - einseitig: Negative Korrelationshypothese "less"
- conf.level: Konfidenzniveau (1 - $\alpha$)
  - default: 0.95

Beispiel

Korrelation item1, item2

cor.test(df_exam$item1, df_exam$item2, method = "pearson",
         alternative = "less", conf.level = .99)

    Pearson's product-moment correlation

data:  df_exam$item1 and df_exam$item2
t = -3.4112, df = 8, p-value = 0.004603
alternative hypothesis: true correlation is less than 0
99 percent confidence interval:
 -1.0000000 -0.1396423
sample estimates:
       cor 
-0.7698004

Produkt-Moment-Korrelation, Hypothese: negative Korrelation, alpha = 1%

cor.test(df_exam$item1, df_exam$item2, method = "pearson",
         alternative = "less", conf.level = .99)

    Pearson's product-moment correlation

data:  df_exam$item1 and df_exam$item2
t = -3.4112, df = 8, p-value = 0.004603
alternative hypothesis: true correlation is less than 0
99 percent confidence interval:
 -1.0000000 -0.1396423
sample estimates:
       cor 
-0.7698004

7.2.1 Matrizen

Werden dataframes (oder Teile dessen) in cov() oder cor() eingefügt, werden Kovarianz- und Korrelationsmatrizen ausgegeben:

cov(df_exam[, 2:4])
           item1      item2      item3
item1  0.6666667 -0.4444444  0.3333333
item2 -0.4444444  0.5000000 -0.2222222
item3  0.3333333 -0.2222222  0.4444444

cor(df_exam[, c("item1", "item2", "item3")], method = "pearson")
           item1      item2      item3
item1  1.0000000 -0.7698004  0.6123724
item2 -0.7698004  1.0000000 -0.4714045
item3  0.6123724 -0.4714045  1.0000000

Funktion corr.test()

corr.test() (Paket psych) liefert inferenzstatistische Berechnungen auch für Korrelationsmatrizen.
corr.test(df, method = "…", adjust = "…", alpha = "…")
- df, method: Siehe cor()
- adjust: Methode zur $\alpha$-Fehler-Adjustierung
  - "none", "bonferroni", …
  - Für weitere siehe ?p.adjust und ?corr.test
- alpha: Signifikanzniveau $\alpha$

library(psych)
corr.test(df_exam[ ,2:4], method = "pearson", adjust = "bonferroni")
Call:corr.test(x = df_exam[, 2:4], method = "pearson", adjust = "bonferroni")
Correlation matrix 
      item1 item2 item3
item1  1.00 -0.77  0.61
item2 -0.77  1.00 -0.47
item3  0.61 -0.47  1.00
Sample Size 
[1] 10
Probability values (Entries above the diagonal are adjusted for multiple tests.) 
      item1 item2 item3
item1  0.00  0.03  0.18
item2  0.01  0.00  0.51
item3  0.06  0.17  0.00

 To see confidence intervals of the correlations, print with the short=FALSE option

Extraktion von Werten

Mit $ können Werte aus der Berechnung extrahiert werden
Dafür Korrelationsmatrix als Objekt speichern
- $se für Extraktion der Standardfehler
- $ci für Extraktion der Konfidenzintervalle
- $p für Extraktion der p-Werte
- $t für Extraktion der t-Werte

Beispiel

Definition eines Objekts mit Inferenzstatistik für df_exam

KorMat <- corr.test(df_exam[ ,2:4], method = "pearson", 
                    adjust = "bonferroni")

Ausgabe Konfidenzintervalle

KorMat$ci
                 lower          r      upper          p
item1-item2 -0.9425738 -0.7698004 -0.2720171 0.00920665
item1-item3 -0.0280809  0.6123724  0.8963838 0.05983788
item2-item3 -0.8490310 -0.4714045  0.2250053 0.16902020

7.3 Lineare Regressionsmodelle

Ziel ist ein Kriterium (abhängige Variable) durch einen Prädiktor (unabhängige Variable) oder einer Kombination aus Prädikatoren für neue Prädikatorenwerte vorherzusagen bzw. den Zusammenhang dieser zu untersuchen.

Allgemeines Vorgehen:

Abhängige und unabhängige Variablen aus Hypothesen ableiten
Skalenniveaus der Variablen bestimmen
Erwarteten Zusammenhang bestimmen
Passendes Regressionsverfahren wählen
Vorraussetzungen prüfen
Regressionsmodell berechnen
Interpretation der Regressionsanalyse

Lineare Regressionsmodelle

Für lineare Regressionen sind folgende Voraussetzungen zu überprüfen:

Es existiert ein linearer Zusammenhang
Erwartungswert der Residuen ist Null
Varianzhomogenität der Residuen (Homoskedastizität)
Die Residuen sind nicht miteinander Korreliert (Autoregression)
Die Residuen sind nicht mit den unabhängigen Variablen korreliert und die unabhängige Variable ist deterministisch(z.B. Omitted-Variable-Bias)
Normalverteilung der Residuen

7.3.1 Modelldefinition

Um eine Regression in R zu rechnen, muss man anhand der vorliegenden Variablen ein Regressionsmodell spezifizieren
Regressionsmodelle werden in sogenannten Formel-Objekten definiert
- Struktur: Abhängige Variable(n) ~ Unabhängige Variable + Unabhängige Variable + …
- Mehrere Variablen werden mit + verbunden
Variablenbezeichnungen entsprechend anpassen
- item1 soll durch item2 und item3 vorhergesagt werden

Beispiel Modelldefinition

model1 <- item1 ~ item2 + item3

7.3.2 Modellschätzung

Anhand des definierten Regressionsmodells und der vorhandenen Daten kann R nun die Modellparameter (inkl. Modellpassung) schätzen
Lineare Regressionsmodelle werden mit lm(formula = …, data = …) geschätzt:
- formula: Definiert das Modell
- data: dataframe, der die Variablen enthält
lm() sollte für die weiteren Berechnungen als Objekt gesichert werden

Beispiel Modellschätzung

Modelldefinition

model1 <- item1 ~ item2 + item3

Modellschätzung und Sicherung in fit1

fit1 <- lm(formula = model1, data = df_exam)

Modell anzeigen

fit1

Call:
lm(formula = model1, data = df_exam)

Coefficients:
(Intercept)        item2        item3  
     2.8929      -0.7143       0.3929

Mit summary() lassen sich detaillierte Informationen zum Regressionsmodell ausgeben:

summary(fit1)

Call:
lm(formula = model1, data = df_exam)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.75000 -0.33036 -0.08929  0.33036  0.64286 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)   2.8929     1.1752   2.462   0.0434 *
item2        -0.7143     0.2832  -2.523   0.0397 *
item3         0.3929     0.3003   1.308   0.2322  
---
Signif. codes:  
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5297 on 7 degrees of freedom
Multiple R-squared:  0.6726,    Adjusted R-squared:  0.5791 
F-statistic: 7.191 on 2 and 7 DF,  p-value: 0.02008

7.3.3 Modellvergleich

Zwei genestete Modelle können mit anova(fit1, fit2) miteinander verglichen werden
- fit1: Ausgangsmodell (restringiertes Modell)
- fit2: Erweitertes Modell (mit zusätzlichen Prädiktoren)

Beispiel Modellvergleich

Modelldefinition und Schätzung

model1 <- item1 ~ item2 + item3
model2 <- item1 ~ item2 + item3 + item4

fit1 <- lm(model1, df_exam)
fit2 <- lm(model2, df_exam)

Modellvergleich, fit1 + fit2

anova(fit1, fit2)
Analysis of Variance Table

Model 1: item1 ~ item2 + item3
Model 2: item1 ~ item2 + item3 + item4
  Res.Df     RSS Df Sum of Sq      F  Pr(>F)  
1      7 1.96429                              
2      6 0.80569  1    1.1586 8.6282 0.02604 *
---
Signif. codes:  
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

7.4 Ergänzungen

7.4.1 Matrizen

Kovarianzmatrizen werden mit cov2cor() in Korrelationsmatrizen umgewandelt:

# Zuweisung
Kova <- cov(df_exam[ , 2:4])
# Berechnung
cov2cor(Kova)
           item1      item2      item3
item1  1.0000000 -0.7698004  0.6123724
item2 -0.7698004  1.0000000 -0.4714045
item3  0.6123724 -0.4714045  1.0000000

7.4.2 Weitere Korrelationen

Mit dem Paket psych können zudem
- Partialkorrelationen (partial.r()),
- tetrachorische (tetrachoric()),
- polychorische (polychoric()),
- biserale (biserial())
- und polyseriale (polyserial()) Korrelationen berechnet werden
Mit dem Paket ppcor können Semipartialkorrelationen berechnet werden

7.4.3 Standartisierte und unstandartisierte Regressionkoeffizienten

Mit coefficients() oder \$coefficients lassen sich die unstandardisierten Regressionskoeffizienten ausgeben
Mit lm.beta() aus dem Paket QuantPsyc lassen sich standardisierte Regressionskoeffizienten ausgeben

# Unstandartisierte Regressionskoeffizienten
coefficients(fit1)
(Intercept)       item2       item3 
  2.8928571  -0.7142857   0.3928571 

# Ausgabe
fit1$coefficients
(Intercept)       item2       item3 
  2.8928571  -0.7142857   0.3928571 

# Standartisierte Regressionskoeffizienten
QuantPsyc::lm.beta(fit1)
     item2      item3 
-0.6185896  0.3207665

7.4.4 Vorhergesagte Werte

predict(), fitted.values() oder \$fitted.values gibt die vorhergesagten Werte für jeden Datenpunkt als Vektor aus:

# Vorhersage Werte, fit1
predict(fit1)
       1        2        3        4        5        6 
2.642857 3.750000 3.357143 2.250000 2.250000 3.357143 
       7        8        9       10 
1.928571 3.750000 3.357143 3.357143 

# Alternative 1
fitted.values(fit1)
       1        2        3        4        5        6 
2.642857 3.750000 3.357143 2.250000 2.250000 3.357143 
       7        8        9       10 
1.928571 3.750000 3.357143 3.357143 

# Alternative 2
fit1$fitted.values
       1        2        3        4        5        6 
2.642857 3.750000 3.357143 2.250000 2.250000 3.357143 
       7        8        9       10 
1.928571 3.750000 3.357143 3.357143

7.4.5 Residuen

resid(), residuals() oder \$residuals gibt die unstandardisierten Residuen pro Datenpunkt aus
rstandard() gibt die standardisierten Residuen aus

# Residuen, fit1
fit1$residuals
          1           2           3           4           5 
 0.35714286  0.25000000 -0.35714286 -0.25000000 -0.25000000 
          6           7           8           9          10 
 0.64285714  0.07142857 -0.75000000 -0.35714286  0.64285714

7.4.6 Modelldefinition

Spezielle Modelle:
- Modell ohne Prädiktoren (Nullmodell): AV ~ 1
- Modell ohne Intercept (Konstante): AV ~ 0 + UV1 + …
- Interaktionsterme (Moderation):
  - AV ~ UV1 + UV2 + UV1*UV2
  - Statt $*$ kann auch $:$ verwendet werden

7.4.7 Hinweise zu weiteren Regressionsmodellen in R

Literatur:
- Fox, J., & Weisberg, S. (2011). An R companion to applied regression. London: SAGE.
- James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning: With applications in R. Springer texts in statistics. New York: Springer.
In R sind viele weitere Verfahren zur Modellselektion, -schätzung und -bewertung umgesetzt wie etwa:
- Bootstrapping
- Kreuzvalidierung
- Shrinkage (Lasse/Ridge) Regression
- Robust Regression
- Power Analyse

7.4.8 General Linear Model (GLM)

glm(forumla, family, data)

Generalisierte lineare Modelle als Verallgemeinerung des linearen Modells $\rightarrow$ Breite Einsatzmöglichkeiten
- formula: Wie bei lm()
- data: Wie bei lm()
- family: Definiert die Zufallsverteilung von Y und die Linkfunktion
Beispiele:
- GLM mit Normalverteilung und ohne besondere Linkfunktion (familiy = gaussian(link = "identity")) $\rightarrow$ Entspricht lm()
- GLM mit Binomialverteilung und logistischer Linkfunktion (family = binomial(link = "logit")) $\rightarrow$ Binär-logistische Regression

7.4.9 Mediation und SEM

Paket lavaan
- Ständig weiterentwickeltes Paket zur Schätzung von Pfad- und Strukturgleichungsmodellen in R
- Ermöglicht auch Bootstrapping-Konfidenzintervalle für indirekte Effekte
- Ausführliche Dokumentation mit Beispielcodes:
  - http://lavaan.ugent.be/tutorial/est.html

7.4.10 Linear Mixed Model (LMM)

Paket lme4
- Liefert eine breite und gut erprobte Palette an Werkzeugen für linear mixed models (Hierarchische lineare Modelle; Mehrebenenmodelle)
- Siehe: Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67(1).
Paket lmerTest
- Reicht Signifikanztests nach, die in lme4 standardmäßig nicht implementiert sind
- https://cran.r-project.org/web/packages/lmerTest/index.html

Handout R-Intensivkurs

7 Tests, Zusammenhangsmaße und Regression

7.1 Statistisches Testen

7.1.1 \(\chi^2\)-Test

7.1.2 t-Test

7.1.3 ANOVA

7.2 Zusammenhangsmaße

7.2.1 Matrizen

7.3 Lineare Regressionsmodelle

7.3.1 Modelldefinition

7.3.2 Modellschätzung

7.3.3 Modellvergleich

7.4 Ergänzungen

7.4.1 Matrizen

7.4.2 Weitere Korrelationen

7.4.3 Standartisierte und unstandartisierte Regressionkoeffizienten

7.4.4 Vorhergesagte Werte

7.4.5 Residuen

7.4.6 Modelldefinition

7.4.7 Hinweise zu weiteren Regressionsmodellen in R

7.4.8 General Linear Model (GLM)

7.4.9 Mediation und SEM

7.4.10 Linear Mixed Model (LMM)